油氣運輸管道以鋼質管道為主，但管道周圍敷設環境復雜，管道受溫度、濕度、紫外線、酸堿性影響勢必會發生腐蝕，導致管壁變薄，甚至穿孔泄漏[1]。國內外學者針對腐蝕管道剩余強度進行了大量研究，如：基于斷裂力學理論推導出用于計算腐蝕管道剩余強度的半經驗公式NG-18[2]；基于有限元分析方法推導計算管道失效壓力的PCORRC方法[3]，該方法相對于早期的公式降低了保守性；基于神經網絡推算出用于計算腐蝕管道剩余強度的IPSO-BPNN算法；基于ASME-B31G腐蝕管道剩余強度評價方法改進的SY/T651-2009標準模型[4]。

由腐蝕管道剩余強度評價模型得到的預測結果與實際值仍存在偏差[1,3,5-7]。針對此類情況，孫寶財等[8-9]將BP神經網絡與遺傳算法相結合，建立了適用于腐蝕管道剩余強度預測的神經網絡算法，該方法提升了模型的準確性，同時也使公式更加簡潔。MOKHTARI等[10]運用理想化腐蝕形狀的估算方法對PCORRC模型和DNV RP-F101模型進行修正，將復雜的腐蝕形狀理想簡化，使公式運用更加方便。以上研究在模型準確性和便捷性方面有所改善，但并未考慮腐蝕管道剩余強度評價模型中各項參數與腐蝕管道實際剩余強度的關聯情況。因此，有學者提出了全概率的修正方法，且這一方法已逐步在纖維復合材料本構模型、纖維與混凝土界面力、黏土中懸臂梁撓度等工程中應用[11-13]。

作者擬采用全概率數學方法解決腐蝕管道剩余強度評價模型的不確定性問題。

1. 模型

1.1 剩余強度評價模型簡介

為預測腐蝕管道剩余強度，建立了大量評價模型[1,4,8-9,14-15]。對于腐蝕管道剩余強度評價模型的選取，一般遵循評價模型的實際運用情況及其在研究中的分析頻率[1,3,6,8,15]。表1為工程中常用的4個評價模型，其分別為DNV RP-F101、PCORRC、SY/T6151-2009、ASME B31G-2012。模型中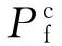為預測剩余強度（計算值），M為膨脹因子，D為管道直徑，t為管道壁厚，L為管道腐蝕長度，d為管道腐蝕深度，σb為管材拉伸強度，σs為管材屈服強度。

早期的評價模型如DNV RP-F101并沒有定義L/Dt2，但這并不代表其準確度不夠。學者們之所以頻繁使用此類型的評價模型是因為簡單的膨脹因子定義使評價模型更加簡潔，使用方便。作者將上述4種模型分別簡稱為D模型、P模型、S模型以及A模型。

1.2 數據收集

腐蝕管道剩余強度受很多因素影響，例如管道自身材料屬性以及管道腐蝕情況[9,14,16]。然而，把所有影響因素都納入考慮范圍并不可行。所以作者選取了6個最為突出的影響因素作為重點參數，它們分別是：管道直徑D、管道壁厚t、管道腐蝕深度d、管道腐蝕長度L、管材拉伸強度σb和管材屈服強度σs[17-18]。本研究以內壓下單一腐蝕狀況為主，將管道剩余強度定義為腐蝕管道實際爆破壓力[19]。從文獻[19-32]中共收集了237組試驗數據用于模型計算。其中，管道直徑范圍為273.00~1 422.40 mm，管道壁厚范圍為4.37~22.90 mm，管道腐蝕深度范圍為1.54~18.55 mm，管道腐蝕長度范圍為4.00~1 420.00 mm，管材拉伸強度范圍為277.40~886.00 MPa，管材屈服強度范圍為240.00~795.00 MPa，實際爆破壓力范圍為4.82~27.50 MPa。

1.3 模型因子

一般情況下，預測模型存在一定的理想化，會忽略實際情況。本研究中，通過定義模型因子來確定理想與實際之間的差距[33]。模型因子（ε）是實際值與預測值的比值，見式（1）。

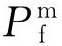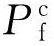式中：和分別為腐蝕管道剩余強度的試驗值（實際值）和預測值。

從式（1）可以看出：ε越接近于1，預測值越接近實際值，表明此模型越準確；ε值遠離1，表明試驗值與預測值相差較大，模型存在較大不確定性。從實際角度分析，ε大于1說明模型是保守的，反之則是不安全的。

將收集的237個腐蝕管道剩余強度的試驗值與4個模型的預測值進行比較，結果如圖1所示。圖中橫縱坐標比值即為模型因子。從圖1可知，模型因子呈兩種類型的散點分布：一種是散亂的分散在45°線周圍，如圖1（c）所示；另一種是緊密分散在45°線下段部分，如圖1（a，b，d）所示。

圖 14種模型的模型因子

Figure 1.Model factors of four types of models

以模型因子為橫坐標，其對應的頻率為縱坐標，繪制4個模型的直方圖，結果如圖2所示。從直方圖可以發現：D模型、P模型以及A模型的模型因子分別集中于1.33、1.38以及1.38附近，這3種評價模型相對保守；S模型的模型因子集中分布在0.85附近。從變異系數（COV）角度來看，4種模型的COV分別是0.29、0.29、0.37、0.29。綜上所述，4種腐蝕管道剩余強度的評價模型都存在不確定性。作者將著重敘述D模型的詳細修正方法，其余評價模型修正方法類似。

圖 24種模型模型因子的直方圖

Figure 2.Column diagrams of model factors from four types of models

從模型因子入手，對腐蝕管道剩余強度評價模型進行修正。模型因子僅反映計算值與實際值的差距，是一個隨機變量，故模型因子的定義必須以隨機性為前提[33-34]，與腐蝕管道剩余強度評價模型中的各參數沒有相關性。通過Spearman法分析各項參數（D、t、d、L、σb、σs）與ε的相關性，包括相關性R和顯著性P兩項評判指標。圖3為管道壁厚與D模型模型因子εD的Spearman分析。結果表明：其R為-0.233，P為0.00，這說明εD與管道壁厚呈負相關。對其余5個參數進行相同處理，所得結果列于表2中。結果表明，εD與6個參數（D、t、d、L、σb、σs）都有相關性，為了減小εD對6個參數的相關性，運用含有以上6個參數的回歸方程f表示模型因子εD。此時的回歸方程f不能完全等同于εD，因為f與實際的εD還存在一定的差距，為此引入殘差因子ε*來修正f與實際εD之間的差值，詳見式（2）。結合式（1）可以得到式（3）。回歸方程f是εD系統部分，故殘差因子ε*是隨機的，與前文中的各參數沒有相關性[12]。對于修正后模型，可以通過判斷殘差因子是否是隨機變量評價其修正效果。故接下來的工作便是找到能系統表示εD的回歸方程f。

圖 3管道壁厚與D模型模型因子的Spearman相關性分析

Figure 3.Spearman correlation analysis of pipe wall thickness versus model factor of model D

2. 結果與討論

2.1 回歸方程擬合

隨機挑選237組數據中的40組數據用于最后驗證f和εD的準確性，剩下的197組數據用于回歸方程的擬合。驗證數據的挑選原則：數據挑選必須是隨機的；數據應盡可能覆蓋不同管道尺寸以及腐蝕情況。由前文可知εD與6個參數存在相關性，使用含有6個參數的回歸方程進行系統擬合表示εD[11]。首先，確認εD與6個參數中每一個參數的相關函數類型即確定核心函數。

在確定核心函數時有很多工況會影響數據的集中，運用平均法處理εD使其散雜的數據集中，找到更好εD與各參數的真實函數關系。例如，當給定條件下管道腐蝕深度為9.00 mm時，有兩組數據符合：D=914.40，t=16.40，d=9.00，σb=813.00，σs=739.00，εD=0.90；D=762.00，t=17.50，d=9.00，σb=557.00，σs=474.00，εD=1.21。

當d為9.00 mm時，εD平均值（記為εDave）為1.06，εDave=（0.90+1.21）/2=1.06。通過類似的做法得到參數d在各種工況下的εDave。對D模型中6個參數（D、t、d、L、σb、σs）做同樣處理，通過此法找到已有工況對應的εDave，結果如圖4所示。其中，空心圓點為平均模型因子εDave。從圖4（f）可以看出，σs與εDave之間關系可以用冪函數來表示。其他參數均可用較高決定系數（R2）的非線性函數表示，為了回歸方程的一致性，用冪函數或指數函數表示各參數的核心函數。

圖 4D模型中各參數與平均模型因子的變化曲線

Figure 4.Curves of parameters with average model factors in mode D: (a) pipe diameter; (b) pipe wall thickness; (c) corrosion depth; (d) corrosion length; (e) tensile strength; (f) yield strength

各參數的核心函數如下所示：；εDave∝b2et；εDave∝b3ed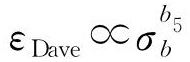；；；。其次，確認各參數核心函數后，將所有核心函數放在一個回歸方程里，建立一個系數與核心函數的乘法模型f，以此表征ε隨輸入參數的系統變化，如式（4）所示。

式中：b0、b1、b2、b3、b4、b5、b6（統稱為bi）為核心函數中的系數，均為未知數。接下來應先確認系數bi。運用SPSS23商業軟件將前文所選的197組數據與εD依照式（4）進行多元線性擬合，計算出未知系數，結果詳見表3。擬合回歸方程的R2為0.62，擬合效果理想。D模型的ε可以表示為

由上文可知，殘差因子ε*是一個隨機量，與之前各參數沒有相關性。使用前文用于驗證的40組數據，對殘差因子ε*進行相關性分析，殘差因子ε*在各種工況下的值由（5）式計算得出。為方便對比，再次運用平均法得到平均殘差因子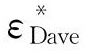。在圖4中用實心黑點表示平均殘差因子。由圖4可見，實心黑點隨機分布在1左右，與原參數的核心函數無關。Spearman相關性分析結果見表2。從表2中可以看出修正后的殘差因子ε*相關系數R處于很低水平，顯著系數P都大于0.05。從結果可以推測出，修正后的εD對6個參數的相關性大大降低。因此，可以說殘差因子ε*是εD的隨機部分。上述回歸方法消除了εD對于參數的依賴性（相關性）。按類似的方法對P模型、S模型以及A模型進行修正，3個模型的未知系數見表3。三個評價模型的ε如下：

2.2 修正前后對比

通過表3中系數得到完整的回歸方程，修正后模型公式如式（9）所示。

式中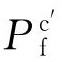：為修正后腐蝕管道剩余強度評價模型的預測值，f由式（4~8）所得。

為便于觀測，以管道剩余強度實際值為橫坐標、修正公式計算的管道剩余強度預測值為縱坐標，繪制散點圖，如圖5所示。修正后4個模型的各項指標列于表4中。由表4可知，D模型的模型因子平均值由修正前1.33降為修正后的1.09，變異系數由0.29降低到0.20；P模型的模型因子平均值由1.38降低到0.96，變異系數由0.29降低到0.21；S模型的模型因子平均值由0.85上升至1.06，變異系數由0.37降低至0.29；A模型的模型因子平均值由1.30降低至0.98，變異系數由0.29降低至0.21。

圖 5修正后各模型的模型因子

Figure 5.Model factors of models after correction

對比圖1和圖5所示修正前后各模型的模型因子可知，修正前模型因子分布在45°直線下方位置，修正后模型因子密集分布在45°線上。這說明全概率法適用于修正腐蝕管道剩余強度評價模型，解決模型的不確定性問題。

3. 結論

運用全概率方法來修正腐蝕管道剩余強度評價模型，解決模型的不確定性。針對應用較為廣泛的4個腐蝕管道剩余強度評價模型（DNV RP-F101、PCORRC、SY/T6151-2009和AMSE B30G-2012），通過237組腐蝕管道爆破試驗數據獲得模型因子（腐蝕管道剩余強度實際值與預測值的比值）。模型因子僅反映可預測性，是一個隨機變量，與腐蝕管道剩余強度評價模型各參數無關。但經Spearman相關性分析發現：4個評價模型的模型因子與評價模型中的各參數（D、t、d、L、σb、σs）有關。

從237組數據中隨機挑選197組試驗數據建立多元回歸方程f替代ε，減小ε與各參數的相關性。又利用剩余的40組數據驗證回歸后殘差因子ε*的隨機性。運用消除相關性校準方法后，4個評價模型的模型因子均值分別為1.09、0.96、1.06、0.98，變異系數分別為0.20、0.21、0.29、0.21。然而未去除相關性的原始評價模型的模型因子均值分別為1.33、1.38、0.85、1.30，變異系數分別為0.29、0.29、0.37、0.29。全概率修正方法適用于解決腐蝕管道剩余強度不確定性問題，并且提高了腐蝕管道剩余強度評價模型的可預測性和精度。

文章來源——材料與測試網